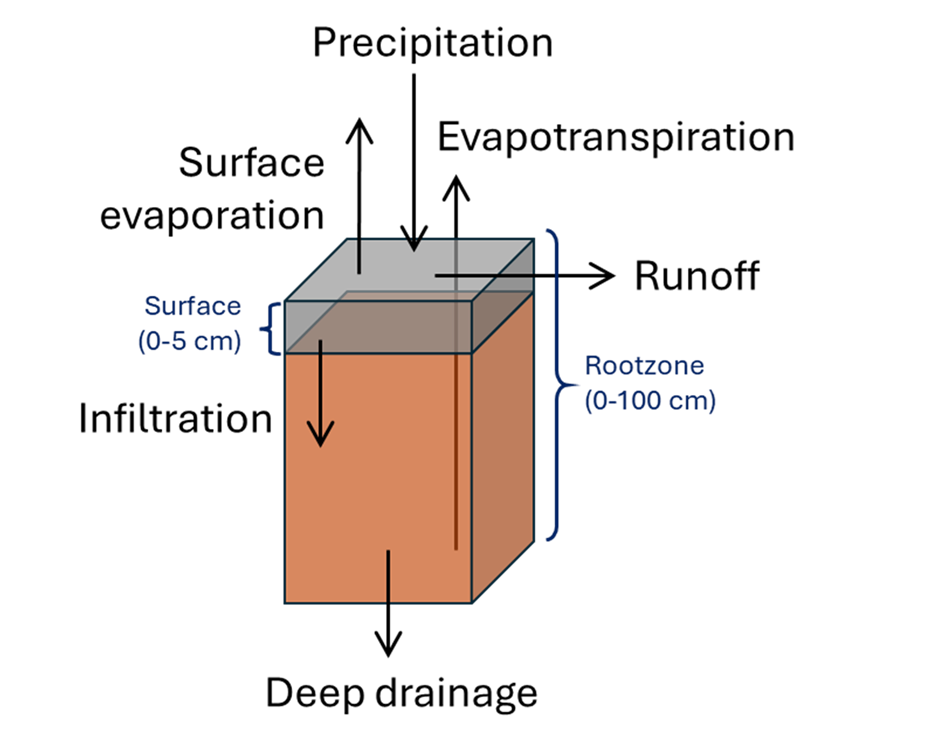
Landscape-scale Soil Hydrology Model is a 2-layer soil water balance model which works based on the emergent signature of terrestrial water-energy coupling beyond the pedon scale scale. As general schematic of the model with key model variables is given below:
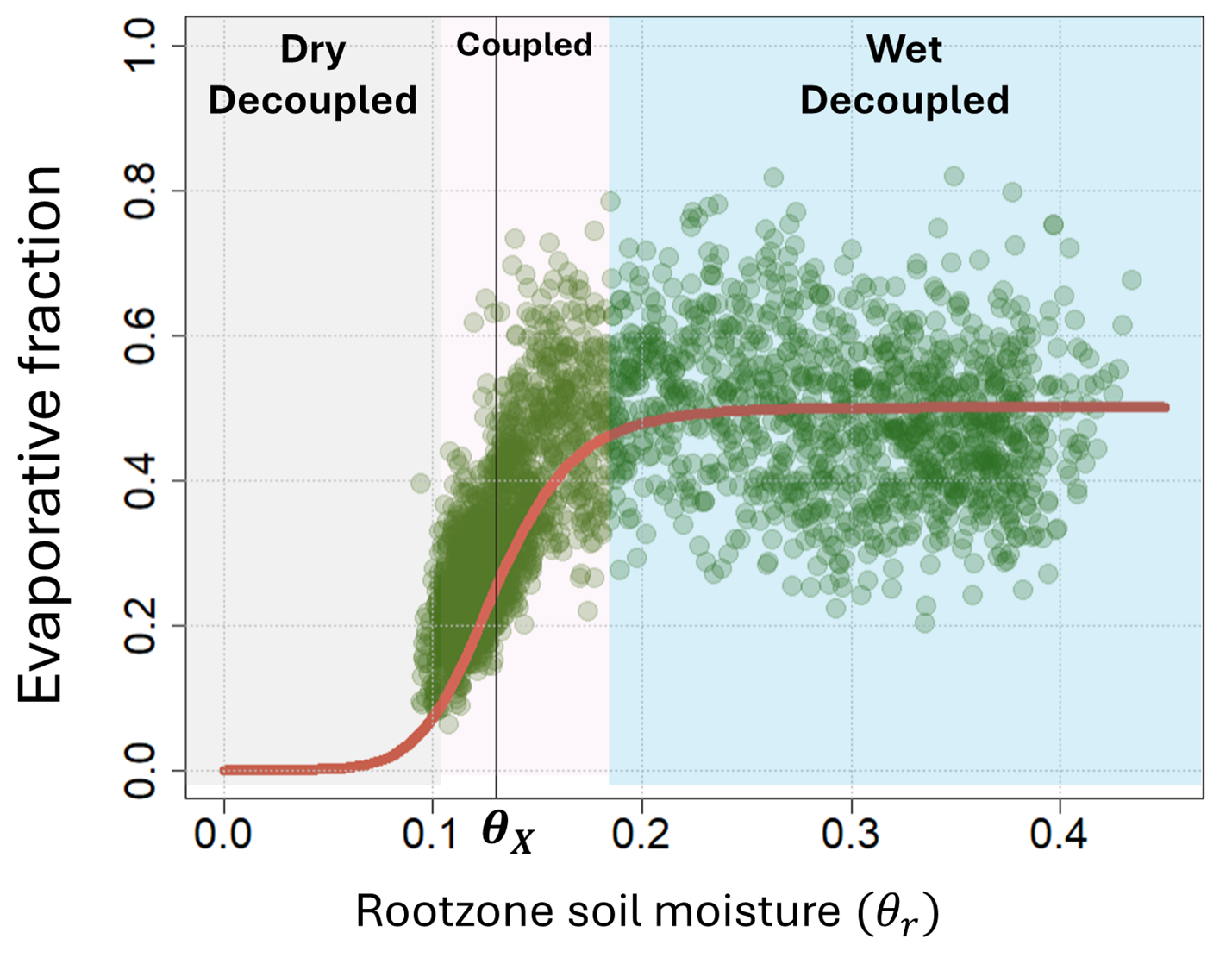
The nature of the soil-vegetation-atmosphere (SVA) interactions evolve with changes in the rootzone soil moisture. This transition of soil hydrologic state from energy-limited to water-limited regimes is represented as a sigmoid curve, with three distinct phases. Abundance of soil moisture in the SVA system can be characterized as wet decoupled, characterized by weakened linkages between water–carbon–energy cycles due to limiting net radiation and atmospheric resistance, with ET losses close to (or at) the potential rate. As the soil begins to dry, soil moisture has higher control over the temporal variability of ET and is characterized by strong land-atmospheric coupling. As soil dries further, soil moisture can not sustain high atmospheric moisture demand, and evapotranspiration again decouples from the rootzone soil moisture.
The connections between soil water balance, noise-induced variability in climatic forces, and positive land-atmospheric feedback lead to dynamic transitions in soil moisture, potentially resulting in a preferred hydrologic states. When one or more state variables are disturbed, or stress (such as atmospheric moisture demand causing evapotranspirative losses) is gradually increased, the SVA system may shift into a new hydrologic regime. Sustained dry-average conditions reinforce dry anomalies (low evaporation results in low regional precipitation and dry soils, leading to even lower evaporation). Conversely, precipitation can alter the soil hydrologic state to wet-average conditions, thereby increasing regional evaporation and precipitation through moisture recycling. If \(\theta_{r}\) represents rootzone soil moisture, then the threshold at which hydrologic tipping of rootzone soil moisture from wet-to-dry-preferential state occurs is represented at \(\theta_{X, r}\), which is called the “tipping” point of the rootzone soil hydrological regimes (Sehgal and Mohanty 2024).
This relationship between rootzone soil moisture and evaporative fraction (evapotranspiration over potential evapotranspiration) is represented as a sigmoid function given below:
\[ EF=\frac{ET}{PET}=\frac{EF_{r,mx}}{\left(1+\left|\left(\frac{\theta_{X, r}\left(\theta_r-1\right)}{\left(1-\theta_{X, r}\right) \theta_r}\right)\right|^m\right)} \]
Here, \(EF_{r,mx}\) represents the maximum evaporative fraction sustainable by the SVA system. The tipping point of soil moisture is represented as \(\theta_{X}\). Land-atmospheric coupling strength is represented by the parameter \(m\). The input vertical flux to the soil below the surface is considered to be derived from the drainage of the surface profile, which is a non-linear function of the field capacity \(\theta_{fc}\), saturated hydraulic conductivity (\(K_{s}\)), porosity (\(\eta\)) and an empirical power coefficient, \(b\). The same equation is adopted for the rootzone to estimate deep drainage.
\[ D=K_S\left(\frac{\left(\max \left(0, \theta-\theta_{f c}\right)\right)}{\eta-\theta_{f c}}\right)^b \]
Surface runoff is estimated as the saturation excess component of the precipitation, based on the hydrologic state of the surface profile. Surface evaporation is considered as a fraction \(Es_{frac}\) of the net evapotranspiration. The depth of the surface and the rootzone profile are fixed and are assumed to be 0-5 and 0-100 cm respectively.
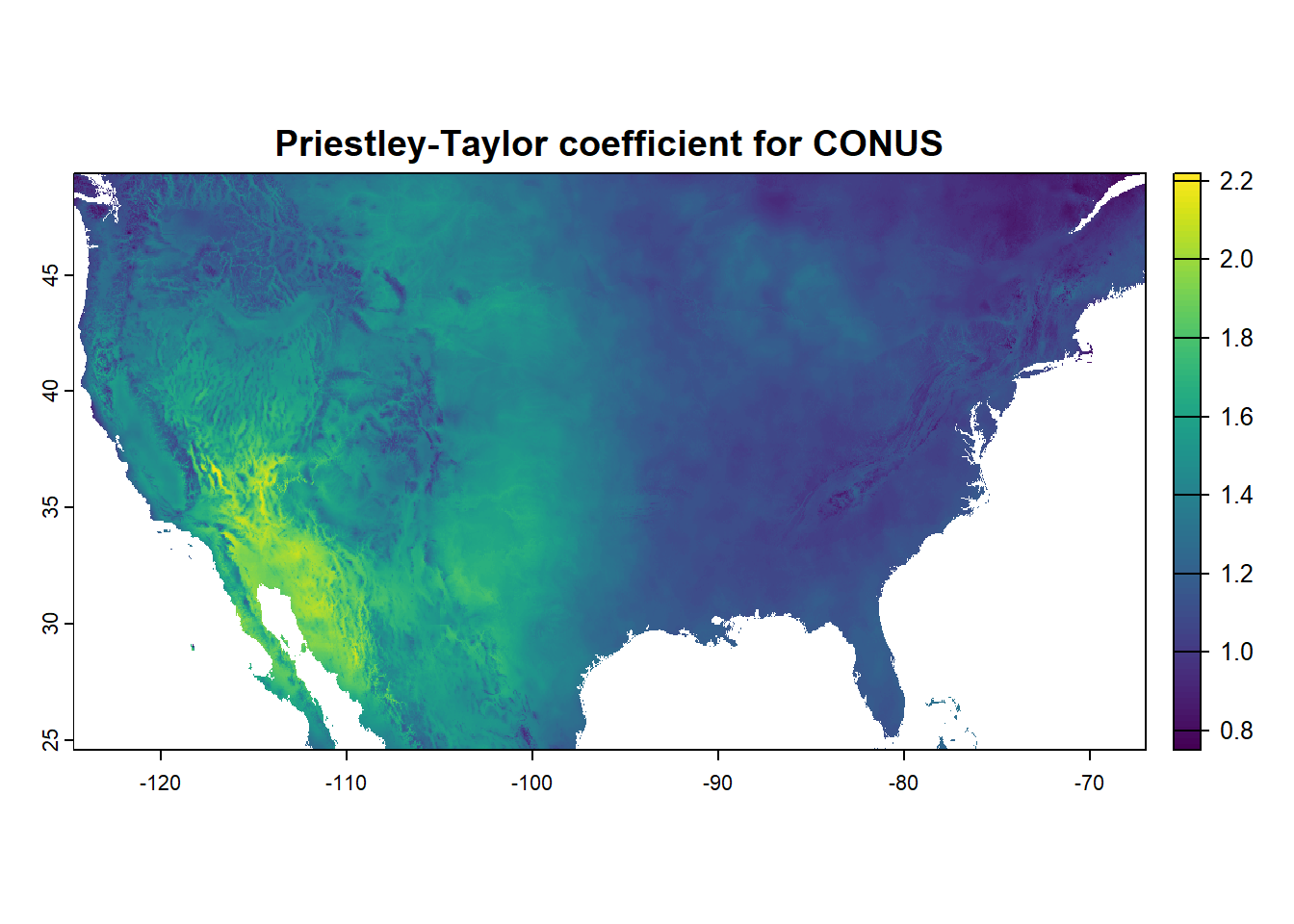
The model uses Priestley-Taylor equation for potential ET estimation. This formulation is based on physical principles and can be seen as a simplified version of the Penman-Monteith formula for calculating evapotranspiration. The simplification involves removing the aerodynamic terms from the Penman-Monteith equation and using a constant (\(α\)), which has been empirically derived and is estimated to be 1.26 for open bodies of water, but can range from <1 (humid conditions) to almost 2 (arid conditions). This constant tends to be higher in arid regions or areas experiencing significant water stress. The Priestley-Taylor formula can be used for calculating daily evapotranspiration and can also be applied to smaller time intervals (hourly, for example) if the necessary data is available.
\[ \text { PET }=\left(\frac{\alpha}{\lambda_v \rho_{\mathrm{w}}}\right) \times \frac{\Delta}{\Delta+\gamma} \times \text {R} \]
if \(T_{mean}< 0^oC\)
\[ \Delta=0.3405 \times \mathrm{e}^\left(0.0642 \mathrm{~T}_{\text {mean}}\right) \\ \]
if \(T_{mean}> 0^oC\) \[ \Delta=0.3221 \times \mathrm{e}^\left(0.0803 \mathrm{~T}_{\mathrm{mean}}^{0.8876}\right) \]
where,
\(PET\)= Daily potential evapotranspiration (\(m\))
\(λv\) = Latent heat of vaporization (2260 \(kJ/kg\))
\(ρw\) = Density of water (1000 \(kg/m^3\))
\(γ\) = Psychrometric constant ( 4.95x \(10^{-4}\) \(kg/m^3/^oC\))
\(Rad\) = Daily solar radiation incident on a horizontal earth surface (\(kg/m^2\))
\(Δ\) = Slope of the saturation vapor density curve from the psychrometric chart (\(kg/^oC\))
\(T_{mean}\) = Daily mean air temperature (\(^oC\))
\(\alpha\) = Priestley-Taylor correction factor
For use with this model, we will use global, high resolution (30arc-sec) estimates of PT correction factor from (Aschonitis et al. 2017). The dataset will be masked to the extent of the region-of-interest at the time of model implementation. Let’s view the values of Priestley-Taylor correction factor for Contiguous US.
library(terra)
utils::download.file("https://github.com/Vinit-Sehgal/SampleData/blob/master/raster_files/priestley_taylor_coefficient/cropPTalpha.tif?raw=true",
destfile = "cropPTalpha.tif",
mode="wb", #wb is write binary
method ='auto',
quiet=FALSE)
PTalpha=rast("cropPTalpha.tif")
plot(PTalpha, main="Priestley-Taylor coefficient for CONUS")
MOPEX (Model Parameter Estimation Experiment, (Schaake, Cong, and Duan 2006)) catchments are a collection of hydrological catchments across the continental United States used for studying and modeling various aspects of hydrology. These catchments are part of a large dataset that includes daily measurements of evaporation, precipitation, streamflow, and temperature, along with other properties such as drainage area, elevation, and slope. The primary goal of the MOPEX initiative is to improve the understanding and prediction of hydrological processes by providing a comprehensive dataset for model calibration and validation. We will use one of the MOPEX catchments in Louisiana for the demonstration of LaSH model at catchment scale (Duan et al. 2006).
library(terra) # for spatial data manipulation
library(mapview) # for spatial data visualization
MOPEX=vect("./SampleData-master/MOPEX/MOPEX_catchments_431.shp")
# Display the MOPEX catchments
mapview(MOPEX, col.regions="blue", lwd=2, legend=TRUE, layer.name="MOPEX Catchments")